【小白渗透入门系列】P5 自动化渗透测试工具
本文共 4126 字,大约阅读时间需要 13 分钟。
大家好!
我是小黄,很高兴又跟大家见面啦 ! 拒绝水文,从我做起 !!!! 未经允许,禁止转载 ,违者必究!!!! 本实验仅适用于学习和测试 ,严禁违法操作 ! ! ! 今天更新的是:- P5 自动化渗透测试工具
- 往期检索:
- 微信公众号回复:【 自动化渗透测试工具 】,即可获取本文全部涉及到的工具。

创建时间:2021年3月3日
软件: MindMaster Pro
自动化渗透测试工具
1. 渗透测试三板斧
1.1 信息搜集(全面了解系统):
- 网络信息(DNS、IP、端口)、服务器信息(操作系统、版本、服务)、中间件(版本)、WEB系统信息(使用技术、部署系统、数据库)、第三方软件(版本)、社工记录(个人邮件地址、泄露账号密码、历史网站信息)
1.2 漏洞利用(占领根据地):
- web漏洞发现、系统漏洞发现、漏洞利用、编写自动漏洞利用脚本、放置隐蔽后门(正常软件漏洞)
1.3 横向扩展(扩大成果,深度挖掘)
- 内网架构分析、攻陷信息中心和数据中心、突破认证服务器(AD域)、内网中间人攻击(获取单点信息)、多级多点后门驻留、长期监视、深度隐蔽
2. 渗透测试标准概述:
2.1 渗透测试步骤:
- 渗透测试分为:前期交互、情报搜集、威胁建模、漏洞分析、渗透攻击、后渗透攻击、报告阶段。
1. 前期交互阶段: 前期交互阶段通常是与客户组织进行讨论,来确定渗透测试的范围和目标。这个阶段最为关键的是需要让客户组织明确清晰地了解渗透测试将涉及哪些目标。选择更加现实可行的渗透测试目标进行实际实施。
2. 情报搜集阶段: 在情报搜集阶段,需要使用各种可能的方法来收集将要攻击的客户组织的所有信息,包括使用社交媒体网络、Google Hacking技术、目标系统踩点等等。作为渗透测试人员,最重要的一项技术就是对目标系统的探查能力,包括获知它的行为模式、运行机理,以及最终可以如何被攻击。 3. 威胁建模阶段: 威胁建模主要使用在情报搜集阶段所获取到的信息,来标识出目标系统上可能存在的安全漏洞与弱点。在进行威胁建模时,确定最为高效的攻击方法、所需要进一步获取到的信息,以及从哪里攻破目标系统。 4. 漏洞分析阶段: 在漏洞分析阶段,综合从前面的几个环节中获取到信息,并从中分析和理解哪些攻击途径回事可行的。特别是需要重点分析端口和漏洞扫描结果,获取到的服务“旗帜”信息,以及在情报搜集环节中得到的其他关键信息。 5. 渗透攻击阶段: 渗透攻击在实际情况下往往没有所预想的那么“一帆风顺”,而往往是“曲径通幽”。最好是在基本能够确信特定渗透攻击会成功的时候,才真正对目标系统实施这次渗透攻击,当然在目标系统中很可能存在着一些没有预期到的安全防护措施,是的这次渗透攻击无法成功。在尝试要触发一个漏洞时,应该清晰地了解在目标系统上存在这个漏洞。 6. 后渗透攻击阶段: 后渗透攻击阶段从已经攻陷了客户组织的一些系统或取得域管理权限之后开始。后渗透攻击阶段将以特定的业务系统作为目标,识别出关键的基础设施,并寻找客户组织最具价值和尝试进行安全保护的信息和资产,当从一个系统攻入另一个系统时,需要演示出能够对客户组织造成最重要业务影响的攻击途径。 7. 报告阶段: 报告是渗透测试过程中最为重要的因素,使用报告文档来交流在渗透测试过程中做了哪些,如何做的,以及最为重要的----客户组织如何修复所发现的安全漏洞和弱点。
2.2 Kali Linux 操作系统:
- Kali Linux是基于Debian的Linux发行版, 设计用于数字取证操作系统。面向专业的渗透测试和安全审计。
- 集成化:预装超过600个渗透测试工具
- 兼容好:Kali可以安装到手机、PC和树莓派等
- 安全性:Kali Linux开发团队由一群可信任的人组成,他们只能在使用多种安全协议的时候提交包或管理源。
- 免费用: Kali Linux一如既往的免费。你永远无需为Kali Linux付费。

3. 信息自动化搜集工具:
3.1 DNS信息搜集工具:
- GOBUSTER: 这款工具基于Go编程语言开发,广大研究人员可使用该工具来对目录、文件、DNS和VHost等对象进行暴力破解攻击。
Usage:
gobuster dns [flags]Flags:
-d, --domain string 指定目标域名 -h, --help 打印帮助信息 -r, --resolver string 指定DNS服务器 -c, --showcname 显示CNAME记录 -i, --showips 显示域名IP --timeout duration 设置超时时间 (默认 1s) --wildcard DNS通配符检测(绕过泛解析)
3.2 IP、端口、系统指纹信息搜集:
- NMAP: NMAP是一款功能强大、界面简洁清晰的连接端口扫描软件。Nmap中文版能够轻松扫描确定哪些服务运行在哪些连接端,并且推断计算机运行哪个操作系统,从而帮助用户管理网络以及评估网络系统安全,堪称系统漏洞扫描之王。
3.3 被动信息搜集:
3.3.1 被动信息收集:
- 公开渠道可获得的信息
- 与目标系统不产生直接交互
- 尽量避免留下一切痕迹
- OSINT:
3.3.2 SHODAN搜索引擎:
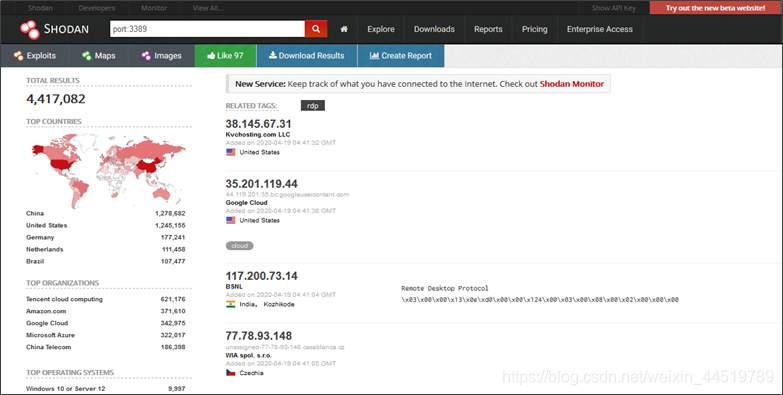
- Shodan 是一个搜索引擎,但它与 Google 这种搜索网址的搜索引擎不同,Shodan 是用来搜索网络空间中在线设备的,你可以通过 Shodan 搜索指定的设备,或者搜索特定类型的设备。
- 具体来说,通过对主机域名、指定端口、指定公司和地区等信息的过滤,Shodan可以找到包括服务器、路由器、摄像头、公共打印机等一系列的物联网设备。
3.3.3 FOFA 搜索引擎:

- FOFA是白帽汇推出的一款国产网络空间资产搜索引擎。它能够帮助用户迅速进行网络资产匹配、加快后续工作进程。例如进行漏洞影响范围分析、应用分布统计、应用流行度排名统计等。
3.3.4 Zoomeye 搜索引擎
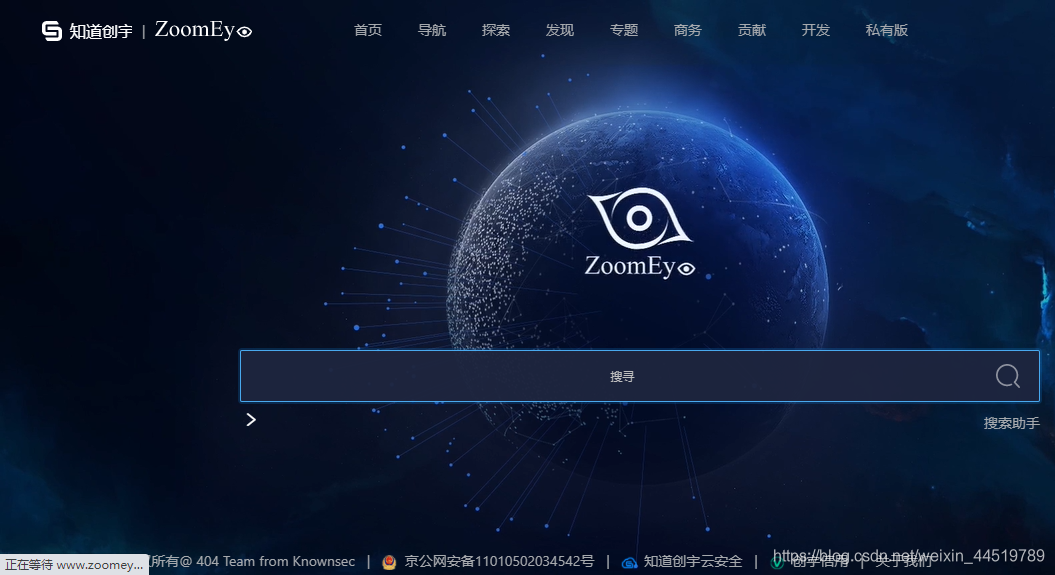

- Zoomeye是知道创宇推出的一款网络空间搜索引擎。
- 它支持公网设备指纹检索和 Web 指纹检索。网站指纹包括应用名、版本、前端框架、后端框架、服务端语言、服务器操作系统、网站容器、内容管理系统和数据库等。设备指纹包括应用名、版本、开放端口、操作系统、服务名、地理位置等。
3.3.5 其实搜集工具:
4. WEB漏洞发现自动化工具:
4.1 半自动web漏洞扫描工具 Burp Suite:
- BurpSuite一款功能强大的渗透测试工具,此软件能够用来分析那些不可预知的应用程序,包括会话令牌和重要数据项的随机性,还可以应用智能感应的网络爬虫,能完整的枚举应用程序的内容和功能。
- BurpSuite 是用于攻击web 应用程序的集成平台,包含了许多工具。Burp Suite为这些工具设计了许多接口,以加快攻击应用程序的过程。所有工具都共享一个请求,并能处理对应的HTTP消息、持久性、认证、代理、日志、警报。
4.2 全自动WEB漏洞扫描工具 AWVS:
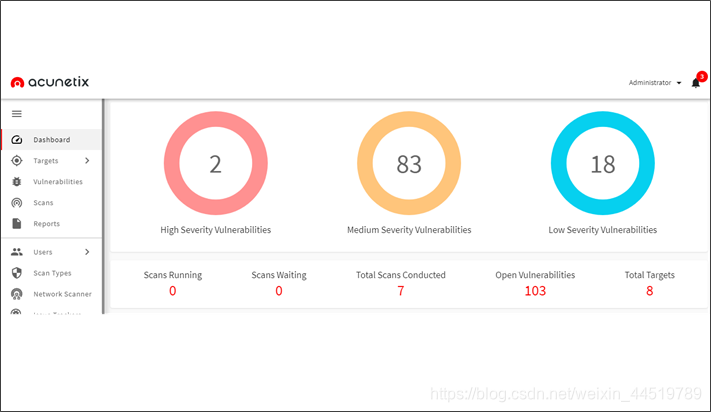
- Acunetix Web Vulnerability Scanner(简称AWVS)是一款知名的商业网络漏洞扫描工具,它通过网络爬虫测试你的网站安全,检测流行安全漏洞。
- 它包含有收费和免费两种版本,目前最新版是V13版本,官方免费下载的是试用14天的版本。
4.3 被动web漏洞扫描工具 W13scan:
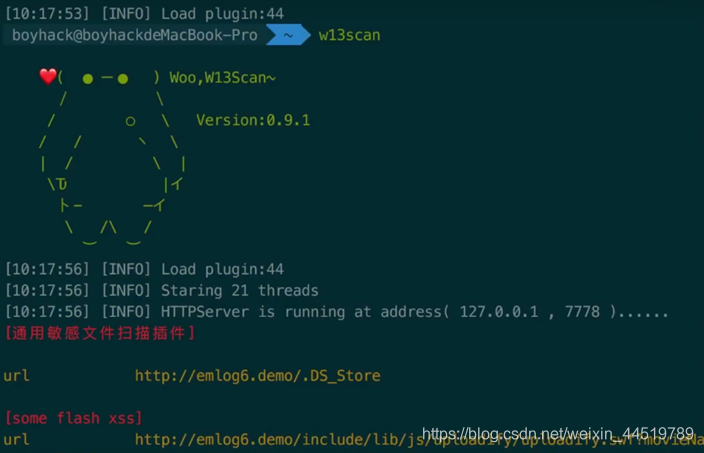
- w13scan是一款插件化基于流量分析的被动扫描器,通过编写插件它会从访问流量中自动扫描。
- w13scan基于Python3进行开发,源代码完全公开,可以加入自己编写的POC扩充漏洞发现能力。
4.4 SQL注入漏洞工具 SQL MAP:
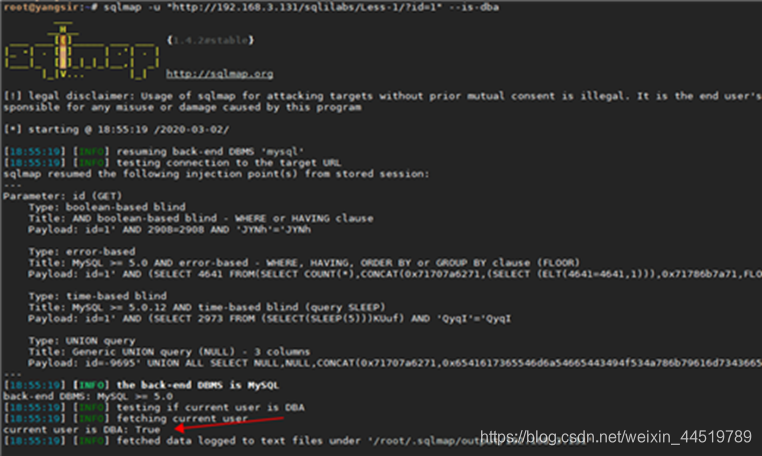
- sqlmap是一个开放源码的sql注入渗透测试工具,其主要功能是扫描、发现并利用给定的URL的SQL注入漏洞,目前支持Access、mssql、mysql、oracle、postgresql多种数据库类型。sqlmap采用四种独特的SQL注入技术,分别是盲推理SQL注入,UNION查询SQL注入,堆查询和基于时间的SQL盲注入。其广泛的功能和选项包括数据库指纹,枚举,数据库提取,访问目标文件系统,并在获取完全操作权限时执行任意命令。
5. 系统漏洞发现自动化工具:
5.1 系统漏洞发现扫描工具 Nessus:
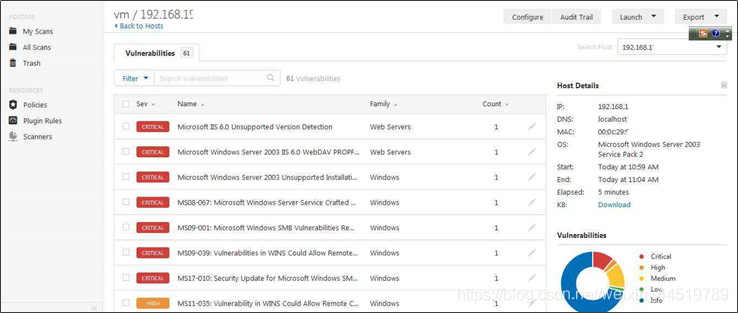
- Nessus 是目前全世界最多人使用的系统漏洞扫描与分析软件。总共有超过75,000个机构使用Nessus作为扫描该机构电脑系统的软件。尽管这个扫描程序可以免费下载得到,但是要从Tenable Network Security更新到所有最新的威胁信息,需要付费后才能获取。在Linux, FreeBSD, Solaris, Mac OSX和Windows系统下都可以使用 Nessus。
5.2 系统漏洞发现扫描工具 searchsploit:
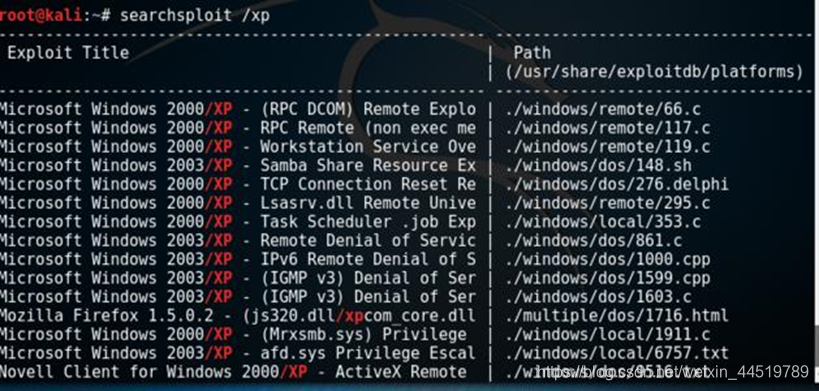
- searchsploit是一个用于Exploit-DB的命令行搜索工具,提供了在本地保存的存储库中执行详细的离线搜索的能力。这种能力特别适用于在没有互联网接入的情况下对网络进行安全评估
5.3 系统漏洞发现扫描工具 searchsploit:
- Metasploit是一个免费的、可下载的框架,通过它可以很容易地获取、开发并对计算机软件漏洞实施攻击。它本身附带数百个已知软件漏洞的专业级漏洞攻击工具。
- Metasploit的设计初衷是打造成一个攻击工具开发平台,本书稍后将讲解如何开发攻击工具。然而在目前情况下,安全专家以及业余安全爱好者更多地将其当作一种点几下鼠标就可以利用其中附带的攻击工具进行成功攻击的环境。
各位路过的朋友,如果觉得可以学到些什么的话,点个赞 再走吧,欢迎各位路过的大佬评论,指正错误,也欢迎有问题的小伙伴评论留言,私信。
每个小伙伴的关注都是本人更新博客的动力!!!
请微信搜索【 在下小黄 】文章更新将在第一时间阅读 !
博客中若有不恰当的地方,请您一定要告诉我。前路崎岖,望我们可以互相帮助,并肩前行!
你可能感兴趣的文章
nestJS学习
查看>>
NetApp凭借领先的混合云数据与服务把握数字化转型机遇
查看>>
NetBeans IDE8.0需要JDK1.7及以上版本
查看>>
netcat的端口转发功能的实现
查看>>
netfilter应用场景
查看>>
netlink2.6.32内核实现源码
查看>>
Netpas:不一样的SD-WAN+ 保障网络通讯品质
查看>>
NetScaler的常用配置
查看>>
netsh advfirewall
查看>>
NETSH WINSOCK RESET这条命令的含义和作用?
查看>>
Netstat端口占用情况
查看>>
Netty WebSocket客户端
查看>>
netty 主要组件+黏包半包+rpc框架+源码透析
查看>>
Netty 异步任务调度与异步线程池
查看>>
Netty中集成Protobuf实现Java对象数据传递
查看>>
netty之 定长数据流处理数据粘包问题
查看>>
Netty事件注册机制深入解析
查看>>
Netty原理分析及实战(四)-客户端与服务端双向通信
查看>>
Netty和Tomcat的区别已经性能对比
查看>>
Netty学习总结(5)——Netty之TCP粘包/拆包问题的解决之道
查看>>